![[object Object]](/_next/image?url=https%3A%2F%2Fcdn.sanity.io%2Fimages%2Fei1axngy%2Fproduction%2Fd192001e06ed413fb0e091ac51bca29248130453-942x942.jpg&w=256&q=75)
by Dr Ana Rojo-Echeburúa
Updated 25 January 2024
What are Gaussian Processes?
![[object Object]](/_next/image?url=https%3A%2F%2Fcdn.sanity.io%2Fimages%2Fei1axngy%2Fproduction%2Fb2ee51cc62f3f0d152e56cfea2a8b90043a4f88d-1280x720.png&w=2048&q=75)
Download the resources for this post here.
Even if you've been exploring machine learning, there's a good chance you haven't come across Gaussian Processes yet. And if you have, you might have found it difficult to grasp the mathematical intuition behind them.
In this series, we're going to dive into the wonderful world of Gaussian Processes.
In this first part of the series, you will learn the basics of Gaussian Processes in a way that's approachable and easy to digest.
✨By the end of this tutorial, you will have a proper understanding of what Gaussian Processes are, how they work behind the scenes, and their main applications.✨
🧠 Key Learnings
First, we introduce Gaussian Processes, a powerful mathematical framework used in machine learning for both regression and classification problems.
Two perspectives on Gaussian Processes are explained: the correlation modelling approach and the distributions over functions approach.
We look into how data collection informs predictions and quantifies uncertainty and discuss the importance of understanding core principles like Bayes theorem, which underpins many predictive models.
We explain how Gaussian Processes are non-parametric and provide flexibility in capturing complex relationships and uncertainty in predictions without predefined parameters. This approach contrasts with traditional curve fitting, offering greater adaptability and flexibility - although these come with their challenges as well.
Finally, we will discuss situations where using Gaussian Processes makes sense. We will also explore some examples and real-world use cases.
🔘 What is a Gaussian Process?
There's something truly fascinating about Gaussian Processes' versatility and all the applications where they are the perfect solution.
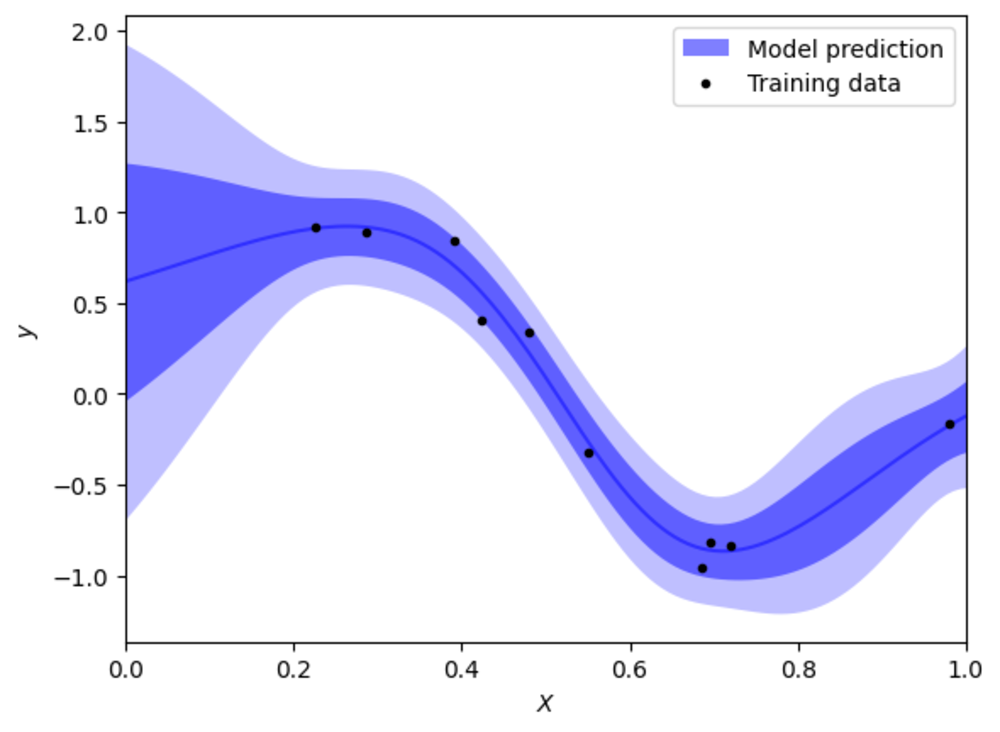
Figure 1. GP
→ But what are they?
A Gaussian Process is a mathematical tool that helps us understand and model relationships in data - but instead of predicting a single value, like saying "the temperature tomorrow is 25 degrees," a Gaussian Process gives us a range of possible values, acknowledging that we're not entirely sure. It's like saying, "I think the temperature is around 25 degrees, but it could be a bit lower or higher."
There are two ways of looking at Gaussian Processes: as a way of Modelling Correlation between Points and as Distributions Over Functions.
Gaussian Processes as a way of Modelling Correlation
To understand this approach, let’s imagine you have booked a holiday to America in autumn and you want to know what the temperature is there then. I know the temperature in Boston in autumn, but even if you ask… I won't tell you the exact value!
Without providing any additional information, you might think, "Well, I could check Google for the average temperature in autumn and its variability” but based on your general knowledge, you might assume a Gaussian distribution centred around 24 degrees - in other words, you're making an educated guess that temperatures are most likely to be around 24 degrees, with fewer occurrences of temperatures deviating significantly from that average.
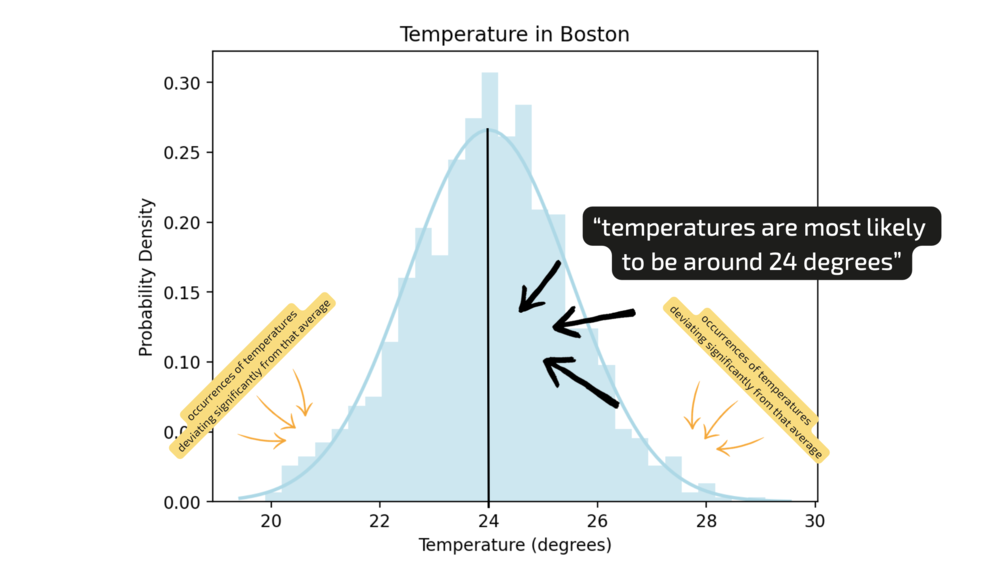
Figure 2. Boston
Now, let's shift to Seattle on the other side of the country. You could estimate a slightly colder temperature, say 20 degrees, with a similar distribution.
You arrive in America, and your first stop is Seattle. Now you actually know the temperature in Seattle - because you are there! - and plan to fly to Boston.
💭 Does that information from Seattle help you predict the temperature in Boston?

Figure 3. Seattle

Figure 4. Map 1
However, if we imagine a line between Seattle and Boston, the closer you get to Boston, the more informative the temperature readings become.
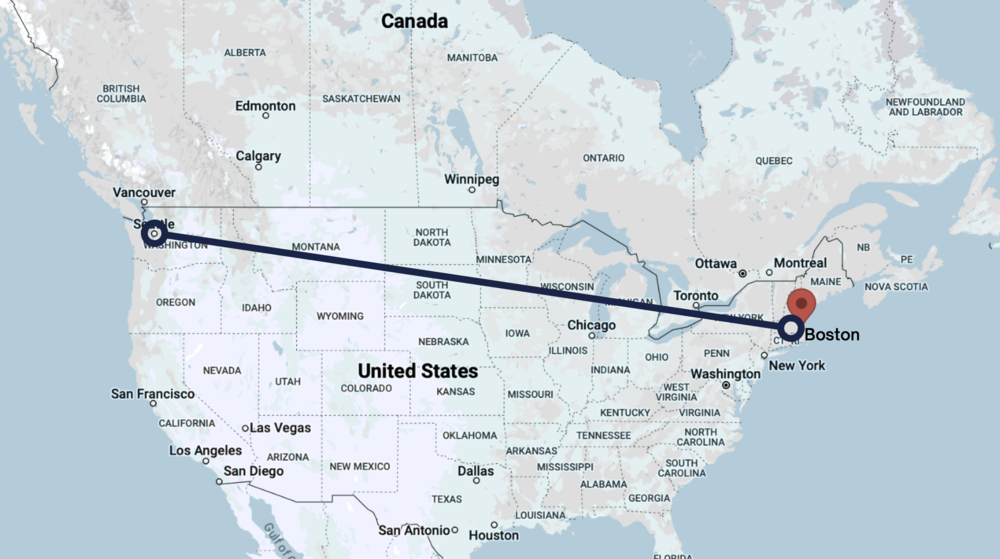
Figure 5. Map 2
For example, if you are 10 miles outside Boston and know the temperature is 24 degrees, you can be reasonably confident it won't be 18 degrees in Boston.
This concept aligns with Gaussian Processes, which don't model the function itself but focus on the correlation between points. They use a covariance function to describe this correlation structure. In simpler terms and using this as an example, it's about understanding how knowing the temperature at one location influences our confidence in predicting the temperature at another location. Factors like distance and historical data help us model this correlation effectively.
Gaussian Processes as Distributions over Functions
Another way of understanding a Gaussian Process is as a distribution over functions, where each function can be thought of as an infinite-dimensional vector.
→ But what does this actually mean?
Imagine you have a set of limited data points representing the temperature of a city at different times of the day over the past month. Now, you want to make predictions for the temperature at different times where you don’t have data points.
We don’t know what happens between some of these points. In other words, there is some uncertainty about what happens there.
So first, you can consider lots of possible curves that could go through these dots, really wiggly ones, really smooth ones, not that wiggly ones, not that smooth ones, etc…
Then, when we make a prediction we want to ask ourselves: “What's the most likely function that goes through that?” while being aware that we don’t have all the information.
After that, we start to collect more data: this restricts the possible functions that could go through it and as a consequence, we reduce our uncertainty.
That's what a Gaussian Process does.
We believe that before we collect any additional data, the possible functions between points have a certain look - and that's my prior.

Figure 6. GP prior
And then we collect data and start restricting the functions that agree with our data.

Figure 7. GP posterior
Now, each of these possible functions, is like an infinite list of numbers. However, since inputs can be any real number, the vector is infinite.
So when we say that a Gaussian Process defines a distribution over functions as infinite-dimensional vectors, it means we're not picking one specific function but considering all possible functions, and for each function, there's an infinite set of values associated with different inputs.
This concept allows Gaussian Processes to capture uncertainty in predictions. Instead of giving a single prediction, they provide a distribution of possible outcomes, which is valuable in scenarios where there might be multiple plausible explanations for the observed data or where uncertainty in predictions is crucial.
🔘 Gaussian Processes and Bayes Theorem
Let’s talk now about Bayes Theorem and how this is a fundamental concept when it comes to understanding Gaussian Processes.
Bayes Theorem provides a way to update our beliefs or probabilities about an event based on new evidence or data. The formula for Bayes' Theorem is expressed as: Here's what each term represents:
- : The probability of event A occurring given that event B has occurred. This is called the posterior probability.
- : The probability of event B occurring given that event A has occurred. This is called the likelihood.
- : The prior probability of event A, representing our initial belief in the probability of A before considering new evidence.
- : The probability of event B occurring.
In simple terms, Bayes' Theorem allows us to update our prior beliefs about the probability of an event A given new evidence B . It provides a structured way to incorporate new information and adjust our beliefs based on observed data.
From a more practical perspective, Bayes' Theorem basically says, "Hey, you're the expert, tell me what could happen based on your knowledge." This initial expert opinion is what we call the prior. Then, we collect real data, and if the data matches our initial opinion, great – things are easy! But if there's a difference, it's okay; we just end up with some uncertainty.
→ Now, here's the thing: if you are familiar with neural networks - if you don’t, don’t worry - it's kind of like they're hardcore data fans. They say, "Give me all your data, I don't care about your opinion, I'm just going to predict."
💭 Bayesian thinking is different.
It's like you have the power to say, "I know the output values should be between 0 and 1, that makes sense." And then, when you see new data, you update your predictions based on evidence. This updated opinion is what we call the "posterior." So, you define your initial thoughts before you even have data (the prior), and then you adjust those thoughts based on what you actually observe (the posterior).
🔘 How do Gaussian Processes Work?
The key idea behind Gaussian Processes is that they allow us to model functions and their uncertainty without explicitly specifying a parametric form for the function.
Instead of defining a fixed set of parameters, a Gaussian Process is characterised by a mean function and a kernel function.
Here:
- represents a function drawn from the Gaussian Process,
- is the mean function, which provides the expected value of the function at a given input ,
- is the kernel, determining how the function values at different inputs and are correlated.
The mean function represents the average behaviour of the function, while the kernel captures how the function values vary with respect to each other across different inputs.
The choice of the kernel depends on the specific requirements of your Gaussian Process model, and different kernels can be chosen based on the characteristics of the underlying data.
One commonly used kernel is the Radial Basis Function (RBF) or Gaussian kernel. Its formula is: Here:
- is the variance parameter, which determines the overall scale of the function.
- is the lengthscale parameter, controlling the "width" or "smoothness" of the kernel.
✨In our next video of the series, we will explore the different kernels that exist and when to use them.✨
However, I wanted to show you one of them so it’s easier to explain why Gaussian processes are non-parametric models. To understand this, let's first explain what a parametric form is.
A parametric form refers to a specific formula with a fixed set of parameters. These parameters determine the shape, behaviour, and characteristics of the function. For example, the parametric form of a straight line in 2D space is given by the equation: where and are parameters that define the slope and y-intercept of the line.
Non-parametric models, on the other hand, do not have a fixed functional form with a predetermined number of parameters.
Gaussian Processes fall into the category of non-parametric models.
That means it doesn't have a fixed number of parameters like some other models. However, it does use parameters to describe its kernel.
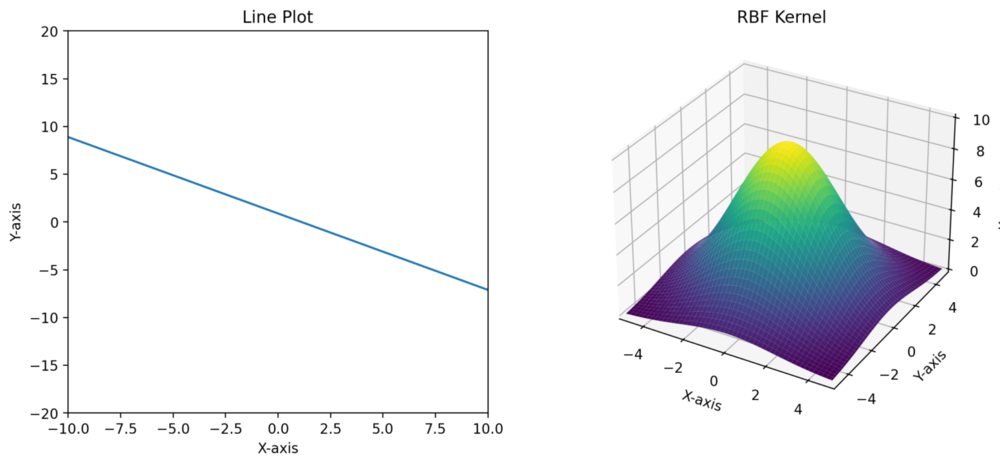
Figure 8. line and kernel
→ Now, why is this different from fitting a curve?
When you fit a curve, you might bias it by choosing a certain form (like a straight line). This is a traditional way, but it lacks flexibility. There are only two parameters, and it's not great for modelling possible correlations.
In the case of a Gaussian Process, you're not defining parameters in the fitting model. Instead, you're modelling possible correlations without specifying parameters for them. So, although people might think it's parametric because of parameters in the kernel, it's not exactly the same.
For instance, in the context of regression, a Gaussian Process might model the relationship between inputs (e.g., time) and outputs (e.g., temperature) without specifying an exact equation. It considers all possible functions that could explain the data and provides a distribution over these functions, capturing uncertainty in the predictions.
A parametric form has a fixed equation with specific parameters, while a non-parametric form, like a Gaussian Process, allows for greater flexibility by not specifying a predetermined equation and capturing uncertainty by considering a distribution over possible functions.
🔘 Recap
▪️A Gaussian Process defines a distribution over functions by saying that the values of the function at different points are jointly Gaussian-distributed. The mean function represents the average behaviour, and the covariance function captures how the values at different points vary together.
▪️This mathematical formulation allows the Gaussian Process to model a wide range of functions while capturing uncertainty in predictions. The specific form of the mean and covariance functions determines the characteristics of the functions in the distribution.
▪️When we say Gaussian Processes allow us to model functions without explicitly specifying a parametric form, it means we are not confined to using a predetermined equation with fixed parameters to represent the function. Instead, Gaussian Processes provide a more flexible approach. Rather than committing to a specific functional form, they define a distribution over all possible functions that could describe the data.
▪️This flexibility is particularly useful in situations where the true underlying function is complex or unknown, and we want the model to learn the functional relationship directly from the data. Gaussian Processes can adapt to the complexity of the data without being limited by a predefined set of parameters, making them valuable for capturing uncertainty in predictions and handling a wide range of functional shapes.
🔘 When do Gaussian Processes Work Best?
Gaussian Processes are particularly valuable in scenarios where data is limited and uncertainty is high due to their ability to provide probabilistic predictions and adapt to the available data.
Here are some examples and use cases:
→ Sparse Data Regression
Example: Predicting the performance of a new chemical compound based on limited experimental data. Use Case: In situations where collecting data is expensive or time-consuming, GPs can model the underlying relationship between inputs and outputs even with a small number of data points. The uncertainty estimates allow practitioners to understand the reliability of the predictions.
→ Surrogate Modeling for Expensive Simulations
Example: Optimising the parameters of a complex simulation model, such as in engineering design or climate modeling. Use Case: GPs can act as surrogate models for computationally expensive simulations. With a few evaluations of the expensive function, the GP can provide predictions and uncertainty estimates, guiding the optimization process efficiently.
→ Bayesian Optimisation
Example: Tuning hyperparameters of machine learning models with a limited budget of evaluations. Use Case: Gaussian Processes are central to Bayesian optimisation, where they model the unknown objective function. The GP guides the optimisation process by suggesting new points to evaluate based on the expected improvement and uncertainty estimates, making it effective in scenarios where function evaluations are resource-intensive.
→ Anomaly Detection
Example: Detecting anomalies in sensor data from industrial equipment. Use Case: In cases where normal behavior is well understood but anomalies are rare, GPs can model the normal behavior and identify deviations. The uncertainty estimates help flag potential anomalies and indicate areas where the model is less confident.
→ Robotics and Autonomous Systems
Example: Trajectory planning for a robot with limited sensor information. Use Case: GPs can be used to model the uncertainty in the robot's perception and environment mapping. This is crucial in scenarios where the robot needs to make decisions with incomplete or noisy information, such as navigating through unknown environments.
In all these cases, the ability of Gaussian Processes to provide not just predictions but also uncertainty estimates is key. This uncertainty information is vital in decision-making processes, allowing us to make informed choices even in situations where the data is sparse or noisy.
In engineering, where experiments can be expensive or time-consuming, Gaussian Processes offer a powerful tool to make informed decisions, optimise designs, and handle uncertainty effectively.
⏭️ What's next?
You can continue your exploring Gaussian Processes on the Streamlit App in the resources section by playing around with the different parameters for each tab.
In the next video of this series, The Kernel Cookbook, we will explore how different kernels define the similarity between data points. We will discuss their definitions, interpretations, and the impact of hyperparameters. We will talk about kernel manipulation and combination techniques, such as adding and multiplying kernels to capture different aspects of the data.I will also give you some tips for choosing the right kernel based on data characteristics.
🤖 Resources
The complete code for the Streamlit App, requirements.txt file and other resources can be downloaded from the resource panel at the top of this article.
Thank you for joining me on this journey. I'm looking forward to seeing you on our next adventure. Until then, happy coding, and goodbye. 👱🏻♀️
Featured Posts
If you found this post helpful, you might enjoy some of these other news updates.
Python In Excel, What Impact Will It Have?
Exploring the likely uses and limitations of Python in Excel

Richard Warburton
Large Scale Uncertainty Quantification
Large Scale Uncertainty Quantification: UM-Bridge makes it easy!

Dr Mikkel Lykkegaard
Expanding our AI Data Assistant to use Prompt Templates and Chains
Part 2 - Using prompt templates, chains and tools to supercharge our assistant's capabilities

Dr Ana Rojo-Echeburúa